이분 탐색(Binary Search) |
이분탐색 혹은 이진탐색이라고 불리며 정렬된 배열에서 원하는 값의 존재여부(혹은 위치)를 찾는 알고리즘이다.
반드시 정렬된 배열에서만 사용 가능하며 탐색을 수행할때마다 검사 범위가 절반으로 줄어들기때문에 시간복잡도 O(logN)이다.
사용 방법 |
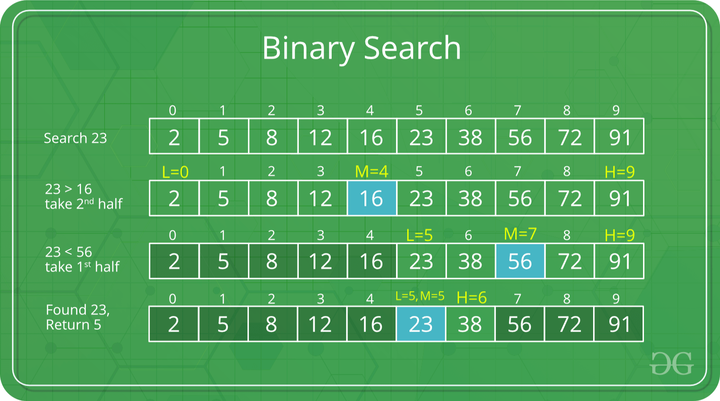
배열의 시작점을 low, 중간점을 mid, 배열의 끝점을 high 정하고 시작
1) 검사 범위에서 mid값이 찾고자 하는 값(target)과 같은지 확인
2) if(arr[mid] == target)이라면 mid를 반환
else if(arr[mid] < target)이라면 검사 범위를 더 큰쪽으로 옮겨야 하므로 low = mid + 1;
else if(arr[mid] > target)이라면 검사 범위를 더 작은쪽으로 옮겨야 하므로 high = mid - 1;
3) 1~2의 과정을 반복하다가 arr[mid] == target이라면 값이 존재하는 것이므로 mid를 반환하면되고
만약 low > high라면 배열에 target이 없는것이므로 return -1;
사용 예시 |
1. 반복문으로 구현
#include <iostream>
#include <vector>
int binarySearch(std::vector<int>& arr, int low, int high, int target) {
while (low <= high) {
int mid = (low + high) / 2;
if (target == arr[mid]) return mid; // 값을 찾았다면 해당 값의 index 반환
else if (target < arr[mid]) high = mid - 1; // 찾는 값이 더 작으면 검사 범위를 작은 쪽으로
else if (target > arr[mid]) low = mid + 1; // 찾는 값이 더 크면 검사 범위를 큰 쪽으로
}
return -1; // 마지막까지 못찾는다면 -1 반환
}
int main()
{
std::vector<int> array{ 1, 3, 5, 7, 9, 11, 13 };
std::cout << "7의 인덱스 : " << binarySearch(array, 0, array.size() - 1, 7) << '\n';
}
2. 재귀로 구현
#include <iostream>
#include <vector>
int binarySearch(std::vector<int>& arr, int low, int high, int target) {
if (low > high) return -1;
int mid = (low + high) / 2;
if (target == arr[mid]) return mid;
else if (target > arr[mid]) return binarySearch(arr, mid + 1, high, target);
else if (target < arr[mid]) return binarySearch(arr, low, mid - 1, target);
}
int main()
{
std::vector<int> array{ 1, 3, 5, 7, 9, 11, 13 };
std::cout << "7의 인덱스 : " << binarySearch(array, 0, array.size() - 1, 7) << '\n';
}
3. C++ STL로 구현
// index 출력은 안되고 존재 유무만 true/false로 알려주는 듯
// algorithm 헤더 include
#include <iostream>
#include <vector>
#include <algorithm>
int main()
{
std::vector<int> array{ 1, 3, 5, 7, 9, 11, 13 };
bool isFound = binary_search(array.begin(), array.end(), 7);
std::cout << std::boolalpha << isFound << '\n';
return 0;
}
이분탐색을 이용한 C++ STL 함수 |
위의 binary_search 외에도 이진탐색을 이용한 STL함수들이 있다.
- lower_bound : 찾고자 하는 값 이상이 처음 나타나는 iterator 반환
- upper_bound : 찾고자 하는 값 초과가 처음 나타나는 iterator 반환
예를들어 { 1, 2, 4, 4, 6, 7 }에 값 4로 위 함수들을 사용한다면
lower_bound는 4가 처음 나타나는 index인 2를 return
upper_bound는 4 초과가 처음 나타나는 index인 4를 return
★두 함수 또한 이진탐색을 기반으로 하므로 정렬된 배열에서만 사용할 수 있다.
이분탐색을 이용한 count
배열 안에서 값 k의 갯수를 구하라고 한다면 count로 for문 돌리면 O(N)이 된다.
반면 lower_bound와 upper_bound를 활용해서 upper - lower를 해주면
해당 배열에 들어있는 k의 갯수를 알 수 있으며 O(logN)이 되므로 더 유리하다.
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> array { 1, 2, 4, 4, 6, 7 };
int target = 4;
int l = lower_bound(array.begin(), array.end(), target) - array.begin();
int u = upper_bound(array.begin(), array.end(), target) - array.begin();
std::cout << l << '\n'; // 2
std::cout << u << '\n'; // 4
// 중복값을 구하는 문제라면
std::cout << "target의 갯수는 " << u - l << "개 입니다.\n";
return 0;
}
이분탐색 vs 선형탐색 |
만약 N = 100인 정렬되지 않은 배열에서 숫자 하나를 찾는다면
이분탐색의 경우 정렬 후에 이분탐색을 해야하니 O(NlogN) + O(logN)이 된다.
시간복잡도에서는 더 큰것만 따지므로 O(NlogN)이라고 했을 때 N = 100이므로 O(100log100)으로 O(200)이 된다.
O(logN)을 생략하지 않고 더해준다고 해도 O(200) + O(log100)이므로 O(202)가 된다.
반면 선형 탐색의 경우 O(N)이므로 O(100)이 될것이다.
그럼 정렬되지 않은 경우는 선형탐색이 유리할까?
위의 예시처럼 N = 100에서 탐색을 한번만 수행한다면 선형탐색은 O(100), 이분탐색은 O(202)가 된다.
그런데 만약 탐색을 한번이 아닌 여러번 수행한다면?
탐색을 한번이 아닌 100번 수행한다면
선형탐색은 O(100)을 100번 수행하므로 O(10000)이 된다.
반면 이분탐색은 먼저 정렬에 O(200)이 들고 그 후부터는 한번의 탐색에 O(log100)인 O(2)의 시간이 든다.
그럼 100번의 탐색을 한다면 O(200) + O(100 * 2)로 O(400)이 된다.
즉 탐색을 한번만 하고 말거라면 선형탐색이 오히려 유리하다.
하지만 여러번 탐색한다면 정렬하는 시간을 한번만 투자해서 이분탐색하는 쪽이 유리하다.
그러므로 상황에 맞게 사용하는 것이 좋겠다.
※ 참고 문헌
https://m42-orion.tistory.com/69
https://www.geeksforgeeks.org/binary-search/
https://velog.io/@junsj119/%EC%9D%B4%EC%A7%84%ED%83%90%EC%83%89Binary-Search