투 포인터 알고리즘(Two Pointers Algorithm)

투 포인터 알고리즘(Two Pointers Algorithm)

 

투 포인터 알고리즘이란 1차원 배열이 있을때 이 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가며 원하는 형태를 얻는 알고리즘  

예를들어 1번 인덱스를 가리키고 있는 left와, 4번인덱스를 가리키고 있는 right가 있다면  
현재 부분배열의 시작점인 left와 현재 부분배열의 끝점인 right 두개의 포인터를 사용해 1~4 부분배열을 나타내는 개념이다.

 

 

사용 예시

 

예제 1) https://www.acmicpc.net/problem/2003

2003번: 수들의 합 2

 

숫자 N개 중 구간의 합이 M이 되는 경우의 수를 구하는 문제이다.

 

만약 누적합 알고리즘을 이용해서 구간 합을 구한다고 하더라도

i번 인덱스에서 0~(i-1)까지 다 빼봐야하고 (i+1)번 인덱스에서도 0~i 인덱스까지 다 빼봐야하고 계속 반복하므로 

시간복잡도가 O(N^2)가 된다.

즉, 좋지 못한 알고리즘이라고 볼 수 있다.

 

그러므로 투포인터를 활용해보자.

※ 각 원소가 자연수이며, M도 자연수라는 조건이 성립하므로 사용할 수 있다.

 

 

아래의 과정을 l < N인 동안 반복

1) 현재 부분합이 M 이상이라면 l++

2) 그렇지 않다면 r++, 단 이미 r == N이라면 종료

3) 현재 부분합이 M과 같으면 결과 ++

 

즉 l, r을 증가시키면서 도중에 (l, r) 부분 배열의 합이 M이 되는 횟수를 count하는 것

 

두 번째 예제 입력인

10 5
1 2 3 4 2 5 3 1 1 2

로 자세히 설명한다면(N = 10, M = 5)

 

초기상태에서는 빨간색 포인터인 l과 파란색 포인터인 r 모두 index 0에 있다.

r이 뒤로 움직일때는 새로 포함된 원소를 sum에 더하고, 

l이 뒤로 움직일때는 빠지게된 원소를 sum에서 빼는 식으로

현재의 l ~ r 구간의 합을 쉽게 구한다.

 

처음엔 sum이 M보다 작으므로 r만 증가시키다가

sum이 M보다 커지는 sum = 6 시점엔 l을 증가시킨다.

 

 

이때 l을 한칸 옮기고 나니 sum == M이므로 result를 1 증가시켜주는 것

 

그리고 다음 값 또한 자연수임을 알고 있으므로 r을 증가시켜봤자 5보다 커진다는것이 명백하므로

sum == M일땐 l을 증가시킨다.

그 후 다시 처음의 과정처럼 r을 증가시키면서 sum이 M보다 크거나 같으면 l을 증가시키는 방식 반복

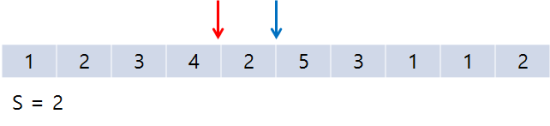
여기서 또 result++

 

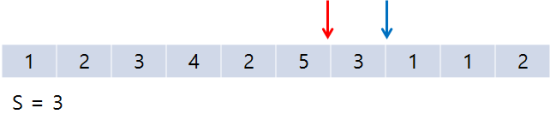
여기서 또 reult++

 

그 후 조건에 맞춰 이동하다보면 r이 배열의 끝을 가리키게 되어 더이상 증가할 수 없게된다.

그럼 루프를 종료시키면 되고

혹은 모두 자연수가 아니라 다른 조건이라면 루프 종료가 아닌 l을 계속 증가시키면 된다.

 

위에서 누적합 알고리즘을 활용한다면 O(N^2)가 된다고 했지만 이런식으로 투포인터 알고리즘을 사용하게 되면 O(N)이 된다.

매 루프마다 두 포인터 중 하나가 1 증가하며, 각 포인터가 끝까지 간다고 해도 l이 N번, r이 N번 가므로 2N번이다.

그러므로 O(N)

 

※ 정답코드

#include <iostream>
#include <vector>

int main()
{
	int N, M;
	std::cin >> N >> M;

	// 배열 입력받기
	std::vector<int> array(N);
	for (int i = 0; i < N; i++) {
		std::cin >> array[i];
	}

	// 누적합 체크하기
	int l = 0, r = 0, sum = 0, result = 0;
	while (true) {
		if (sum >= M) { // 과정 1) 현재 부분합이 M 이상이라면 l++
			sum -= array[l++]; 
		}
		else if (sum < M) { // 과정 2) 그렇지 않다면 r++, 단 이미 r == N이라면 종료
			if (r == N) break;
			sum += array[r++];
		}

		if (sum == M) result++;	// 과정 3) 현재 부분합이 M과 같으면 결과 ++
	}

	std::cout << result;

	return 0;
}

 

 

 

 

※ 참고문헌

https://blog.naver.com/kks227/220795165570